幂函数游戏,从基础到应用

亲爱的数学迷们，今天我要带你们走进一个充满魔力的世界——幂函数游戏！想象你手中有一把神奇的魔法钥匙，可以打开无数数学宝库的大门。而这把钥匙，就是幂函数。准备好了吗？让我们一起踏上这场奇妙的数学之旅吧！

幂函数：魔法钥匙的诞生

在数学的海洋里，有一种函数，它像一位神秘的魔法师，能够将数字变幻出无穷无尽的魔力。这种函数，就是幂函数。它长这样：\\( y = x^a \\)，其中 \\( x \\) 是底数，\\( a \\) 是指数。别看它简单，却蕴含着无尽的奥秘。

幂函数游戏：一场数学的冒险

想象你是一名勇敢的探险家，手中拿着这把魔法钥匙，准备去解开数学世界的秘密。而这场冒险，就是幂函数游戏。

游戏规则

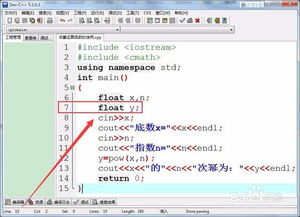
1. 寻找规律：观察幂函数的图像，你会发现，当底数 \\( x \\) 不变，指数 \\( a \\) 变化时，图像会发生怎样的变化？

2. 探索性质：研究幂函数的定义域、值域、奇偶性、单调性等性质，看看它们如何影响函数的图像。

3. 解决实际问题：运用幂函数解决实际问题，比如计算物体的运动速度、计算利息等。

游戏玩法

1. 绘制图像：使用直角坐标系，绘制不同底数和指数的幂函数图像，观察它们的形状和特点。

2. 分析性质：根据图像，分析幂函数的定义域、值域、奇偶性、单调性等性质。

3. 解决挑战：尝试解决一些与幂函数相关的实际问题，比如计算物体的运动速度、计算利息等。

幂函数游戏：一场数学的盛宴

在这场游戏中，你将体验到数学的无限魅力。下面，让我们一起来品尝这场盛宴的美食吧！

1. 幂函数的图像

当底数 \\( x \\) 不变，指数 \\( a \\) 变化时，幂函数的图像会发生怎样的变化呢？

- 当 \\( a > 0 \\) 时，图像呈现指数增长的趋势，随着 \\( x \\) 的增大，\\( y \\) 的值会迅速增大。

- 当 \\( a < 0 \\) 时，图像呈现指数衰减的趋势，随着 \\( x \\) 的增大，\\( y \\) 的值会迅速减小。

- 当 \\( a = 0 \\) 时，图像呈现水平直线，\\( y \\) 的值始终为 1。

2. 幂函数的性质

幂函数具有以下性质：

- 定义域：当 \\( a \\) 为正整数时，定义域为 \\( x > 0 \\)；当 \\( a \\) 为负整数时，定义域为 \\( x \

eq 0 \\)。

- 值域：当 \\( a \\) 为正整数时，值域为 \\( y > 0 \\)；当 \\( a \\) 为负整数时，值域为 \\( y \

eq 0 \\)。

- 奇偶性：当 \\( a \\) 为奇数时，函数为奇函数；当 \\( a \\) 为偶数时，函数为偶函数。

- 单调性：当 \\( a > 0 \\) 时，函数在定义域内单调递增；当 \\( a < 0 \\) 时，函数在定义域内单调递减。

3. 解决实际问题

运用幂函数解决实际问题，比如计算物体的运动速度、计算利息等。

- 计算物体的运动速度：假设一个物体以 \\( v \\) 的速度匀速直线运动，经过 \\( t \\) 秒后，它所行驶的距离 \\( s \\) 可以用公式 \\( s = v \\times t \\) 来计算。这里的 \\( v \\) 和 \\( t \\) 都是变量，而 \\( s \\) 是它们的幂函数。

- 计算利息：假设你将 \\( P \\) 元钱存入银行，年利率为 \\( r \\)，存期为 \\( t \\) 年，那么 \\( t \\) 年后，你将获得的利息 \\( I \\) 可以用公式 \\( I = P \\times r \\times t \\) 来计算。这里的 \\( P \\)、\\( r \\) 和 \\( t \\) 都是变量，而 \\( I \\) 是它们的幂函数。

幂函数游戏：一场数学的狂欢

在这场游戏中，你不仅能够体验到数学的无限魅力，还能锻炼自己的逻辑思维和问题解决能力。当你解开一个又一个数学谜题时，你会感受到一种前所未有的成就感。

亲爱的数学迷们，让我们一起拿起这把魔法钥匙，开启幂函数游戏的大门吧！在这场奇妙的数学之旅中，你将收获知识、快乐和成长